Cynical Nation

In the latest installment of my math-blogging series (see previous posts here and here), I'm continuing to explore paradoxes of the infinite, working toward the goal of understanding the Banach-Tarski paradox.

This is one I came up with myself when I was bored in calculus class one day. I'm going to calculate how long it takes for a rubber ball to bounce an infinite number of times. No, really.

You know how it is when you bounce a ball. With each bounce, the ball loses energy and only rises to a fraction of its original height. As the height of each bounce diminishes, so does the time it takes for the bounce to complete. Towards the end, the ball bounces very, very quickly, accelerating to culminate in a bunch of frenzied, tiny little bounces in the last second, just before it stops entirely.

Consider a ball that returns to exactly one-half its original height each time you bounce it. You drop it from a height of one meter initially, it bounces back up to a height of 50 cm, then to 25 cm, then 12.5 and so on. Theoretically, the ball will bounce an infinite number of times. In the real world, of course, we know it doesn't really bounce infinitely many times, for a number of reasons. Eventually, for example, the altitude of the bounce would become smaller than the physical imperfections on the surface of the ball, causing the bouncing to stop.

As usual, however, we're going to set aside such practical considerations and consider the theoretical case. How long then, would it take for a ball to bounce infinitely many times? The answer might surprise you.

In Physics 101, we learn that the time it takes for a ball to be dropped from a height h is

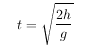
where g is the gravitational acceleration constant, 9.8 meters per second squared. The time it takes to fall, hit the floor, and then bounce back up to half its initial height is then

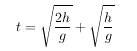
Similarly, we can add up the time required for all the bounces to take place:

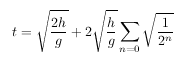
The coefficient 2 in front of the summation represents the "round trip" all subsequent bounces must take -- up, then back down. We can actually calculate this sum by taking the following integral:

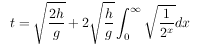
The result of this calculation (if I did it right) is

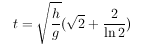
Now I didn't bother to calculate how many seconds this corresponds to, but that isn't really the point. The point is that the answer is a finite number. Depending on the initial height you drop the ball from, it may take 3 seconds, 5 seconds, 7.2532 seconds or some other amount of time for the ball to stop bouncing. But the point is that after a finite period of time, the ball will have actually bounced an infinite number of times -- theoretically, at least. Far out, huh?

This isn't directly related to Banach-Tarski, other than the fact that both problems are examples of how infinite numbers can lead to bizarre and non-intuitive results. The next examples I'll show here are going to be a bit more set theoretical in nature, as they get us closer and closer to the kind of thinking required to look at Banach-Tarski. More later.