Banach-Tarski: Paradoxes of the infinite
A few days ago I began a series of posts regarding the Banach-Tarski paradox. The implications of this paradox, that it's possible to decompose a sphere into a finite number of pieces and reassemble them to form two solid spheres equal in size to the original, has never set well with me.
One of the keys to understanding Banach-Tarski is understanding that a mathematical sphere is infinitely divisible, and can be divided into infinitely complex subsets. In part, Banach-Tarski is a paradox of the infinite.
Paradoxes and bizarre, counter-intuitive results go hand-in-hand with the study of transfinite sets. My goal now is to start getting us accustomed to such paradoxes, and to proceed from there to an understanding of Banach-Tarski.
I'm going to skip Zeno's paradoxes, because frankly, they're kind of stupid. Everyone knows you can catch the damn turtle. Anyway, Zeno is taught in freshman calculus as a way to demonstrate that a sum of infinitely many infinitesimally small quantities can be finite. Let's just forget Zeno and move on to a more interesting example.
One of the main things they teach you in second semester calculus is how to calculate the volumes and surface areas of some highly improbably shapes.
Let's consider a simple function: the reciprocal function, 1/x.
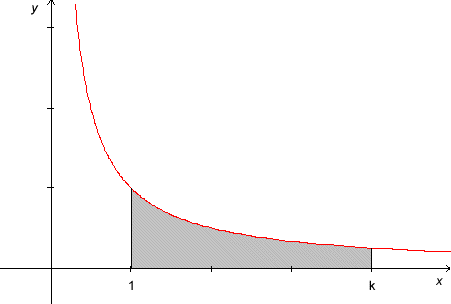
Cool chart, huh? Now what if we formed a surface by rotating this line around the x-axis. It would sweep out a cool cone shape.
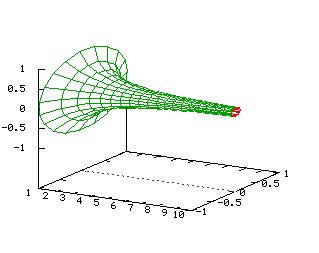
It's a fairly straightforward exercise in integral calculus to determine the volume and surface area of this cone for a value of x equal to k:
A = 2&pi ln k
V = π (1 - 1/k)
Now consider what happens as we let k approach infinity. The surface area of this cone approaches infinity, as we'd expect. The cone's volume, however, approaches π.
So what does that mean? We have a cone with an infinite surface but a finite volume. Does that mean that we can fill it up with paint, but we can't paint it? Or does that mean that we can paint an infinite surface with a finite volume of paint simply by pouring it into the cone?
Yes, there are easily a dozen reasons why this wouldn't work: Paint is made of discrete molecules, and beyond a certain point, paint molecules would be too large to go any further down the cone. Coats of paint are not infinitely thin, but have a finite thickness, so the paint would be used up before it got to the nether regions of the cone.
That's all true, of course, but... isn't there still something unsettling about this result, even after you've made excuses for the real world?
Anyway, weird, huh? There's more to come. We'll explore a few more such oddities before tacking Banach-Tarski directly.
Comments
Ooooh, fun!
Perhaps I'm thinking too visually (and keep in mind that I have absolutely no education in calculas) but it seems as though as K approaches infinity, the cone would get narrower and narrower until, after a certain point, the tip would stretch out but it would have grown so narrow that there was no space in the middle beyond that point.
So it would then make sense that you could have an infinite number of possible surface areas, since the tip could keep going forever, with a finite number of possible volumes, since the tip would essentially "close up" after a while.
Am I close?
Posted by: Adam | March 8, 2006 09:19 PM
OK Barry, now you're scaring me.
I'm still struggling over the basis for the initial theory.
And yes, I AM wearing my dunce cap.
Posted by: JMK | March 8, 2006 09:30 PM
Yeah, you've pretty much got it, Adam. Still weirds me out, though.
Posted by: BNJ | March 9, 2006 08:37 AM
way, way, way above my pay grade--and intelligence level.
Barry, put away the brown acid, will ya?
Posted by: fred | March 9, 2006 08:55 AM
Yeah, one of the things I've learned recently is that when you're dealing with infinity all bets are off. Math stops caring what your sensible intuitions are and starts getting rowdy and doing all kinds of unsettling things...
Posted by: Matt McIntosh | March 9, 2006 12:46 PM
this stuff is akin to when I used to get roasted and then try to think back to what it was like before time began...too scary after a while, so I'd run and hide in the bathroom.
Posted by: fred | March 9, 2006 01:40 PM
When was this, last week?
Posted by: BNJ | March 9, 2006 01:43 PM
months probably; these days, all I do is blow my ears out with loud music, before falling asleep
Posted by: fred | March 9, 2006 02:32 PM
Do I get one of those star-stickers that teachers hand out for being good?
Do I? DO I??
Posted by: Adam | March 10, 2006 07:53 AM
Actually Adam, you are incorrect and could get a silver sticker for being close. If you read carefully, as k approaches infinity, the volume approaches pi, but never really gets there because k never gets to infinity. infinity is a concept, more of a bound than a number or value.
Also, no matter how thin the cone gets on the tail, the surface has no thickness, therefore there is still a tiny bit of volume in that part of the cone.
The reason you can calculate a finite value for the volume is because in certain cases, the sum of an infinate amount of finite values can be finite. See the geometric series.
I look forward to more of these posts.
Posted by: Joel | July 15, 2008 04:15 PM